|
|
|
A generalization of the Riemann Zeta Function with a Formula
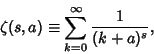 |
(1) |
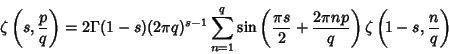 |
(2) |
| (3) |
![\begin{displaymath}
\zeta(z,a) = {2\Gamma(1-z)\over (2\pi)^{1-z}}\left[{\sin\lef...
...}\right)\sum_{n=1}^\infty{\sin(2\pi an)\over n^{1-z}}}\right].
\end{displaymath}](h_1943.gif) |
(4) |
| (5) | |||
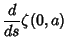 |
(6) | ||
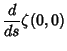 |
(7) |
| (8) |
For Positive integers ![]() ,
, ![]() , and
, and ![]() ,
,
|
|
|
|
|
|
|
|
(9) |
|
|
(10) |
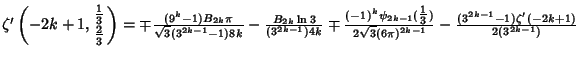
|
(11) |
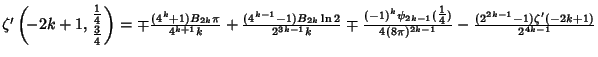
|
(12) |
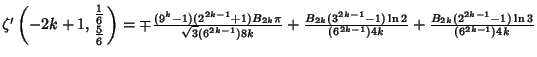
|
|
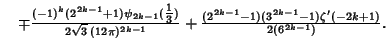
|
(13) |
See also Khintchine's Constant, Polygamma Function, Psi Function, Riemann Zeta Function, Zeta Function
References
Apostol, T. M. Introduction to Analytic Number Theory. New York: Springer-Verlag, 1995.
Elizalde, E.; Odintsov, A. D.; and Romeo, A. Zeta Regularization Techniques with Applications.
River Edge, NJ: World Scientific, 1994.
Knopfmacher, J. ``Generalised Euler Constants.'' Proc. Edinburgh Math. Soc. 21, 25-32, 1978.
Magnus, W. and Oberhettinger, F. Formulas and Theorems for the Special Functions of Mathematical Physics, 3rd ed.
New York: Springer-Verlag, 1966.
Miller, J. and Adamchik, V. ``Derivatives of the Hurwitz Zeta Function for Rational Arguments.'' Submitted to
J. Symb. Comput.
Spanier, J. and Oldham, K. B. ``The Hurwitz Function
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University
Press, pp. 268-269, 1950.
![]() .''
Ch. 62 in An Atlas of Functions.
Washington, DC: Hemisphere, pp. 653-664, 1987.
.''
Ch. 62 in An Atlas of Functions.
Washington, DC: Hemisphere, pp. 653-664, 1987.
|
|
|
© 1996-9 Eric W. Weisstein