A function also called the Sampling Function and defined by
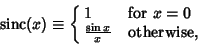 |
(1) |
where 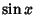 is the Sine function. Let
is the Sine function. Let 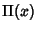 be the Rectangle Function, then the Fourier Transform
of
be the Rectangle Function, then the Fourier Transform
of 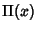 is the sinc function
is the sinc function
![\begin{displaymath}
{\mathcal F}[\Pi(x)]=\mathop{\rm sinc}\nolimits (\pi k).
\end{displaymath}](s1_1379.gif) |
(2) |
The sinc function therefore frequently arises in physical applications such as
Fourier transform spectroscopy  as the so-called Instrument Function, which gives the instrumental
response to a Delta Function input. Removing the instrument functions from the final spectrum requires use of some
sort of Deconvolution algorithm.
as the so-called Instrument Function, which gives the instrumental
response to a Delta Function input. Removing the instrument functions from the final spectrum requires use of some
sort of Deconvolution algorithm.
The sinc function can be written as a complex Integral by noting that
The sinc function can also be written as the Infinite Product
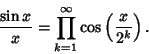 |
(4) |
Definite integrals involving the sinc function include
These are all special cases of the amazing general result
![\begin{displaymath}
\int_0^\infty {\sin^a x\over x^b}\,dx = {\pi^{1-c}(-1)^{\lef...
...\right\rfloor -c} (-1)^k{a\choose k}(a-2k)^{b-1}[\ln(a-2k)]^c,
\end{displaymath}](s1_1393.gif) |
(10) |
where 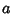 and
and 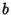 are Positive integers such that
are Positive integers such that 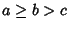 ,
,
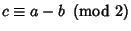 ,
,
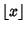 is the Floor Function,
and
is the Floor Function,
and  is taken to be equal to 1 (Kogan). This spectacular formula simplifies in the special case when
is taken to be equal to 1 (Kogan). This spectacular formula simplifies in the special case when 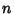 is a Positive
Even integer to
is a Positive
Even integer to
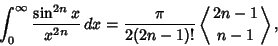 |
(11) |
where
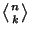 is an Eulerian Number (Kogan). The solution of the integral can also be written in terms of the
Recurrence Relation for the coefficients
is an Eulerian Number (Kogan). The solution of the integral can also be written in terms of the
Recurrence Relation for the coefficients
![\begin{displaymath}
c(a,b)=\cases{
{\pi\over 2^{a+1-b}}{a-1\choose {\textstyle{...
... (b-1)(b-2)} [(a-1)c(a-2,b-2)-a\cdot c(a,b-2)] & otherwise\cr}
\end{displaymath}](s1_1399.gif) |
(12) |
(Zimmerman).
The half-infinite integral of
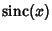 can be derived using Contour Integration.
In the above figure, consider the path
can be derived using Contour Integration.
In the above figure, consider the path
 . Now write
. Now write
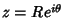 . On an arc,
. On an arc,
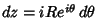 and on the x-Axis,
and on the x-Axis,
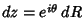 . Write
. Write
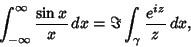 |
(13) |
where 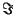 denotes the Imaginary Point. Now define
denotes the Imaginary Point. Now define
where the second and fourth terms use the identities 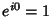 and
and 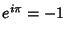 . Simplifying,
. Simplifying,
where the third term vanishes by Jordan's Lemma. Performing the integration of the first term and combining the
others yield
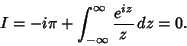 |
(16) |
Rearranging gives
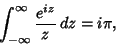 |
(17) |
so
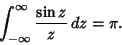 |
(18) |
The same result is arrived at using the method of Residues by noting
so
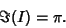 |
(20) |
Since the integrand is symmetric, we therefore have
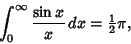 |
(21) |
giving the Sine Integral evaluated at 0 as
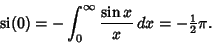 |
(22) |
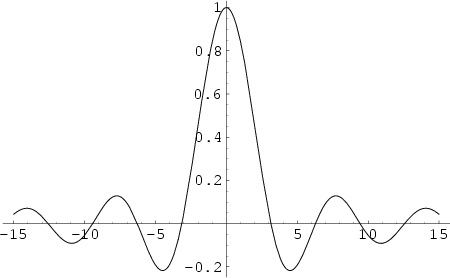
An interesting property of
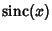 is that the set of Local Extrema of
is that the set of Local Extrema of
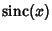 corresponds
to its intersections with the Cosine function
corresponds
to its intersections with the Cosine function 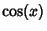 , as illustrated above.
, as illustrated above.
See also Fourier Transform, Fourier Transform--Rectangle Function,
Instrument Function, Jinc Function, Sine, Sine Integral
References
Kogan, S. ``A Note on Definite Integrals Involving Trigonometric Functions.''
http://www.mathsoft.com/asolve/constant/pi/sin/sin.html.
Morrison, K. E. ``Cosine Products, Fourier Transforms, and Random Sums.'' Amer. Math. Monthly 102, 716-724, 1995.
© 1996-9 Eric W. Weisstein
1999-05-26

![$\displaystyle {1\over 2inx} [e^{itx}]^n_{-n} = {1\over 2n} \int^n_{-n} e^{ixt}\,dt.$](s1_1382.gif)
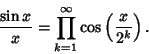
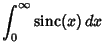
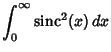
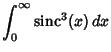
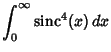
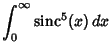
![\begin{displaymath}
\int_0^\infty {\sin^a x\over x^b}\,dx = {\pi^{1-c}(-1)^{\lef...
...\right\rfloor -c} (-1)^k{a\choose k}(a-2k)^{b-1}[\ln(a-2k)]^c,
\end{displaymath}](s1_1393.gif)
![\begin{displaymath}
c(a,b)=\cases{
{\pi\over 2^{a+1-b}}{a-1\choose {\textstyle{...
... (b-1)(b-2)} [(a-1)c(a-2,b-2)-a\cdot c(a,b-2)] & otherwise\cr}
\end{displaymath}](s1_1399.gif)
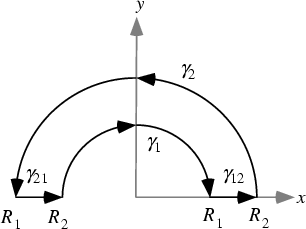
![]() can be derived using Contour Integration.
In the above figure, consider the path
can be derived using Contour Integration.
In the above figure, consider the path
![]() . Now write
. Now write
![]() . On an arc,
. On an arc,
![]() and on the x-Axis,
and on the x-Axis,
![]() . Write
. Write
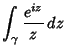
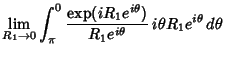
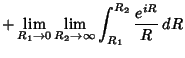
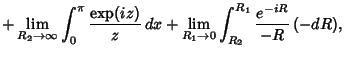
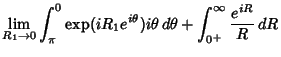
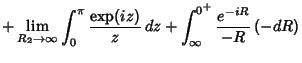
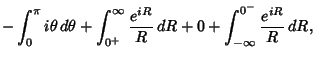
![$\displaystyle i\pi\left[{(z-0) {e^{iz}\over z}}\right]_{z=0} = i\pi [e^{iz}]_{z=0}$](s1_1422.gif)
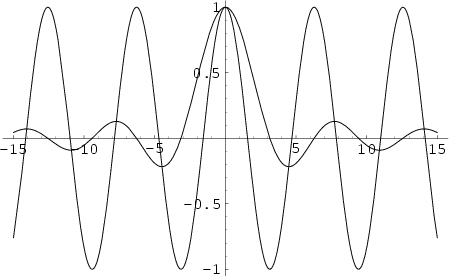
![]() is that the set of Local Extrema of
is that the set of Local Extrema of
![]() corresponds
to its intersections with the Cosine function
corresponds
to its intersections with the Cosine function ![]() , as illustrated above.
, as illustrated above.