|
|
|
The function
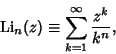 |
(1) |
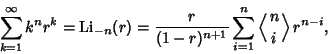 |
(2) |
The polylogarithm satisfies the fundamental identities
| (3) |
| (4) |
| (5) |
![\begin{displaymath}
\left[{{d\over ds} \mathop{\rm Li}\nolimits _s(-1)}\right]_{...
...tyle{1\over 2}}\ln(2\pi)=\ln\left({\sqrt{2\over\pi}\,}\right).
\end{displaymath}](p2_1437.gif) |
(6) |
The polylogarithm identities lead to remarkable expressions. Ramanujan ![]() gave the polylogarithm identities
gave the polylogarithm identities
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
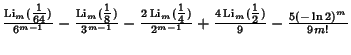
|
|
|
|
(17) |
No general Algorithm is know for the integration of polylogarithms of functions.
See also Dilogarithm, Eulerian Number, Legendre's Chi-Function, Logarithmic Integral, Nielsen-Ramanujan Constants
References
Bailey, D.; Borwein, P.; and Plouffe, S. ``On the Rapid Computation of Various Polylogarithmic Constants.''
http://www.cecm.sfu.ca/~pborwein/PAPERS/P123.ps.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 323-326, 1994.
Lewin, L. Polylogarithms and Associated Functions. New York: North-Holland, 1981.
Lewin, L. (Ed.). Structural Properties of Polylogarithms. Providence, RI: Amer. Math. Soc., 1991.
Nielsen, N. Der Euler'sche Dilogarithms. Leipzig, Germany: Halle, 1909.
|
|
|
© 1996-9 Eric W. Weisstein