|
|
|
Polynomials related to the Brahmagupta Polynomials. They are defined by the
Recurrence Relations
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
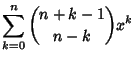 |
(6) | ||
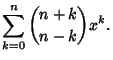 |
(7) |
Defining the Matrix
| (8) |
| (9) |
| (10) |
Defining
| (11) | |||
| (12) |
![$\displaystyle {\sin[(n+1)\theta]\over\sin\theta}$](m_1903.gif) |
(13) | ||
![$\displaystyle {\sinh[(n+1)\phi]\over\sinh\phi}$](m_1904.gif) |
(14) |
![$\displaystyle {\cos[{\textstyle{1\over 2}}(2n+1)\theta]\over\cos({\textstyle{1\over 2}}\theta)}$](m_1905.gif) |
(15) | ||
![$\displaystyle {\cosh[{\textstyle{1\over 2}}(2n+1)\phi]\over\cosh({\textstyle{1\over 2}}\theta)}.$](m_1906.gif) |
(16) |
The Morgan-Voyce polynomials are related to the Fibonacci Polynomials ![]() by
by
| (17) | |||
| (18) |
![]() satisfies the Ordinary Differential Equation
satisfies the Ordinary Differential Equation
| (19) |
| (20) |
See also Brahmagupta Polynomial, Fibonacci Polynomial
References
Lahr, J. ``Fibonacci and Lucas Numbers and the Morgan-Voyce Polynomials in Ladder Networks and in Electric Line
Theory.'' In Fibonacci Numbers and Their Applications (Ed. G. E. Bergum, A. N. Philippou, and A. F. Horadam).
Dordrecht, Netherlands: Reidel, 1986.
Morgan-Voyce, A. M. ``Ladder Network Analysis Using Fibonacci Numbers.'' IRE Trans. Circuit Th. CT-6, 321-322, Sep. 1959.
Swamy, M. N. S. ``Properties of the Polynomials Defined by Morgan-Voyce.'' Fib. Quart. 4, 73-81, 1966.
Swamy, M. N. S. ``More Fibonacci Identities.'' Fib. Quart. 4, 369-372, 1966.
Swamy, M. N. S. ``Further Properties of Morgan-Voyce Polynomials.'' Fib. Quart. 6, 167-175, 1968.
|
|
|
© 1996-9 Eric W. Weisstein