Chapter 20
Elementary Number Theory
This chapter briefly introduces the basic knowledge of elementary number theory . It is divided into six sections . The first five sections discuss the properties of integers and the method of division , continuous fractions and Fibonacci sequences , congruence and Sun Tzu's theorem , and introduce several important The number-theoretic functions and Mobius transforms of algebraic numbers are listed , and the discrimination methods of several types of irreducible polynomials are listed . The last section gives a brief introduction to the basic concepts and properties of algebraic numbers .
§ 1 Integer
[ Integer part and fractional part ] Let a be a real number , the largest integer not exceeding a is called the integer part of α , denoted as . And called the fractional part of a .![]()
![]()
For example , , etc. ![]()
![]()
![]()
The integer part has the following relation :
![]()
![]()
![]() , n is a natural number
, n is a natural number
![]() , n is a natural number
, n is a natural number
![]()
![]() or
or ![]()
Note that the meaning of "rounding operation" in computer programs is different from the meaning of "integer part" here : it was consistent at the time ; it was inconsistent at the time , for example , but after rounding on the computer .![]()
![]()
![]()
![]()
![]()
[ Divisibility ] If there is an integer c , such that the integers a and b are suitable for
![]()
Then b is said to be divisible by a , denoted as . In this case, a is called a multiple of b , and b is called a factor ( or submultiple ) of a.![]()
If b is not divisible by a , it is recorded as b a .![]()
Divisibility has the following properties ( the following equations ):![]()
1 ° If , , then ; ![]()
![]()
![]()
2 ° If , then ; ![]()
![]()
3 ° If , , then for any integer m,n we have ![]()
![]()
![]()
4 ° If b is a true factor ( ie ) of a, then ![]()
![]()
[ Prime numbers and Eratos sieve method ] An integer greater than 1 that has exactly 1 and itself two natural numbers as its factors is called a prime number , denoted as . Except for 2 , which is an even prime number , the other prime numbers are odd numbers .![]()
Prime numbers have the properties :
There are infinitely many 1 ° prime numbers . If the number of prime numbers not exceeding the natural number n is denoted as p (n) , then at that time , there is * , and further there are ![]()
![]()
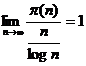
2 ° Let p be a prime number , if , then or . ![]()
![]()
![]()
The power of the square containing the prime number p in 3 ° is equal to ![]()
![]()
4 ° If it is a positive integer , it cannot be divisible by all prime numbers not exceeding , then n must be a prime number . This method of judging whether a natural number is a prime number is called the Eratosian sieve method . This method can establish a prime number table . ![]()
![]()
[ Unique Decomposition Theorem ] All natural numbers greater than 1 can be uniquely decomposed into the product of prime powers . If , is a natural number , then n can be uniquely represented as![]()
![]()
![]() ( for natural numbers )
( for natural numbers )
![]() ( for prime numbers )
( for prime numbers )
This is called the standard decomposition of n . The number s of different prime factors in n does not exceed .![]()
Obviously , any natural number n can be expressed as
![]() ( k,m are natural numbers or zero )
( k,m are natural numbers or zero )
This expression is unique .
[ Mason number ] integer
![]() ( p is a prime number )
( p is a prime number )
Those who are prime numbers are called Meissen numbers . So far only 27 have been found , namely
![]()
Whether there are infinite Meissen numbers has not yet been proved .
[ Fermat number ] integer
![]() ( n is a natural number )
( n is a natural number )
It is called the Fermat number . So far, only 5 Fermat numbers have been found to be prime , namely
![]()
None of the following 46 Fermat numbers are prime :
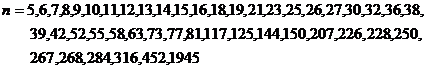
[ Reversing and dividing method * ] Each integer a can be uniquely represented by a positive integer b as
![]()
In the formula, q is called the incomplete quotient obtained by dividing a by b , and r is called the remainder obtained by dividing a by b . The rolling division method refers to the following finite series of equations :
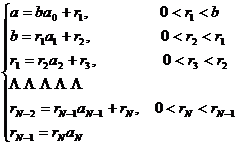 ( 1 )
( 1 )
Example 1 set a = 525, b = 231, according to the formula (1) , the following formulas and formulas can be listed :
arithmetic grass _
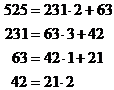
![]()
![]()
![]()
[ The greatest common factor and the least common multiple ] Let a and b be integers . A positive integer that can divide both a and b is called the common factor of a and b , and the largest one is called the greatest common factor of a and b * , denoted as _![]()
![]()
Especially at that time , it is said that a and b are mutually prime .![]()
Let a and b be positive integers . A positive integer that is divisible by both a and b is called the common multiple of a and b, and the smallest one is called the least common multiple of a and b * , which is written as![]()
![]()
Let n positive integers , and define their greatest common factor by induction as![]()
![]()
Its least common multiple is
![]()
The greatest common factor and the least common multiple have the following properties :
1 ° There are integers x, y, such that x , y can be specifically obtained by the rolling division method . It is also obtained by a series of equations of the rolling division method , namely ![]()
![]()
![]()
![]()
Example 2 obtains (525,231)=21 from Example 1. Because the formula from Example 1 has
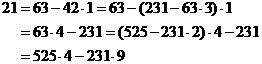
So we get x = 4, y = - 9 .
2 ° must exist for any two integers x, y . ![]()
3 ° If , , then . ![]()
![]()
![]()
4 ° if then ![]()
![]()
If , then![]()
![]()
5 ° If a and b are two positive integers , they are their prime factors , and the standard decomposition formulas are ![]()
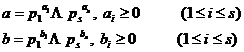
![]()
but

6 ° ![]()
If 7 ° is a co-prime positive integer , that is , then ![]()
![]()
![]()