§ 5 Bessel function
1.
Bessel functions of the first kind
[ Definition and Expression of Bessel Functions of the First Kind ]
![]()
is called a Bessel function of the first order, and it is single-valued in the plane except the semi-real axis (and when integer, in the full plane) . It satisfies the Bessel differential equation![]()
![]()
![]()
![]()
![]()
![]()
The constants (real or complex) in an equation are called the order of the equation or the order of the solution .![]()
When (integer), is the generating function:![]()
![]()
![]()
![]() =
=![]()
and have
![]()
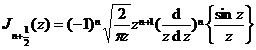
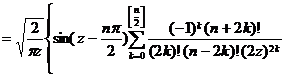

![]()
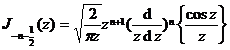
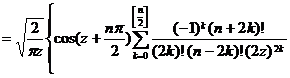

![]()
![]()
![]()
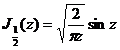


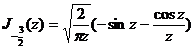
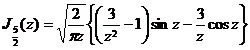
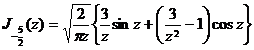
[ integral expression ]
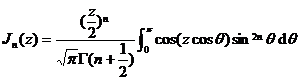 (Poisson integral representation)
(Poisson integral representation)
![]() (represented by Bessel integral)
(represented by Bessel integral)

![]()
![]()
![]()
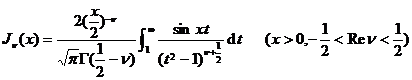
![]()
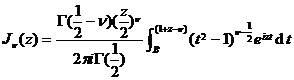
|
|
![]() at the point,
at the point,![]()
![]()
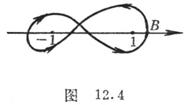
The integral route is in the shape of “ ” as shown in the figure, at the point![]()
![]()
![]()
![]()
![]()
[ Related formula ] ![]()
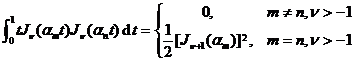
where are the two positive zeros of the function .![]()
![]()
![]()
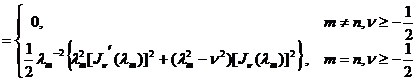
where are the two positive zeros of the function , and are any given constant .![]()
![]()
![]()
![]()
![]() (addition formula)
(addition formula)
![]()
where and represents the distance from the origin to any two points on the plane , and is the angle of intersection of the sum .![]()
![]()
![]()
![]()
![]()
![]()
![]()
[ asymptotic expression ]
![]()
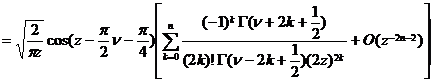
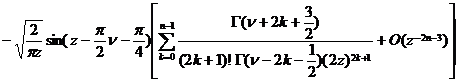
![]() fixed,
fixed,![]()
![]()
![]() fixed,
fixed,![]()
![]()
![]()
![]()
![]()
![]()
![]()
 (in
(in![]()
Second,
the second kind of Bessel function (Neumann function)
[ Definition and other expressions of Bessel functions of the second kind ]
![]()
It is called the Bessel function of the second kind ( also recorded in some books ), also known as the Neumann function, which is also the solution of the Bessel differential equation ( 1 ), where it is the Bessel function of the first kind ,![]()
![]()
![]()
![]()
![]() and single-valued analysis in the plane excluding the semi-real axis .
and single-valued analysis in the plane excluding the semi-real axis .![]()
![]()
![]()
![]()
![]() integer)
integer)
![]()
![]()
![]() is Euler's constant)
is Euler's constant)
![]()

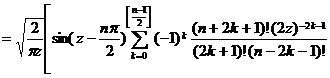
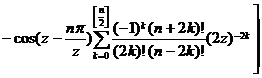
![]()
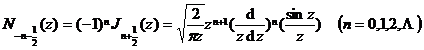
![]()
![]()
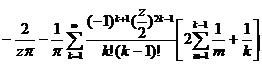
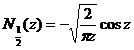

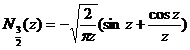
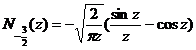
[ integral expression ]
![]()
![]()
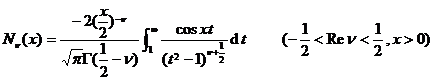
![]()
![]()
![]()
[ asymptotic expression ]
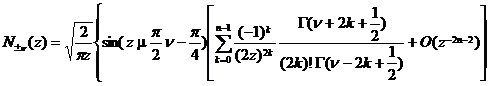

![]() fixed,
fixed,![]()
![]()
![]()
![]()
Third,
the third kind of Bessel function (Hankel function)
[ Definition and Expression of Bessel Functions of the Third Kind ]
![]()
![]()
![]()
are called Bessel functions of the third kind, and Hankel functions of the first and second kinds, respectively, are single-valued analytically in the plane except the semi-real axis and satisfy the Bessel differential equation ( 1 ) .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

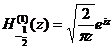
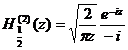
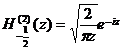
[ integral expression ]
![]()
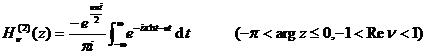

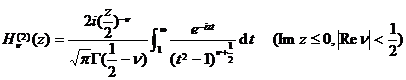

![]()
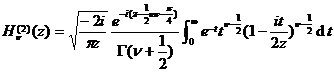
![]()
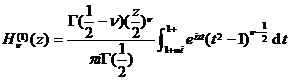
|
|
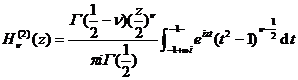
![]() positive integer,
positive integer,![]()
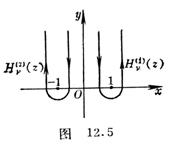
The integral route is shown in Figure 12.5.
[ asymptotic expression ]
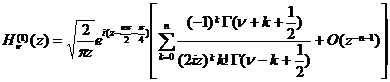
![]() fixed,
fixed,![]()
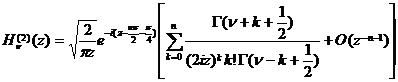
![]() fixed,
fixed,![]()
![]()
![]()
![]()
![]()
![]()
![]()
Fourth,
the relationship between various Bessel functions and related formulas
[ Self-recursion relation ] The following represents the Bessel function and .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
[ Relationship between various Bessel functions ]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
[ Other related formulas ]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5.
Variant Bessel function
[ Definition and Expression of Variant Bessel Function ]
![]()
![]()
![]()
Variant Bessel functions of the first and second kinds, also known as Basset functions, respectively, are single-valued in the plane with the semi-real axis removed .![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ( as a positive integer)
( as a positive integer)![]()
![]()
![]()
![]()
![]() is Euler's constant)
is Euler's constant)
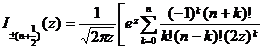
![]()

![]()
![]()
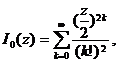
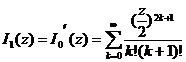
![]()
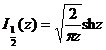
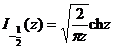
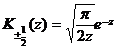
![]()

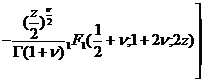
![]()
[ integral expression ]
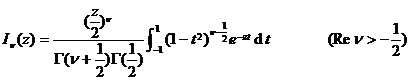
![]()
![]()
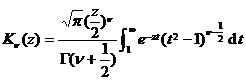
![]()
![]()
![]()

![]()

![]() is an integer)
is an integer)
[ Related formula ]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
[ asymptotic expression ]
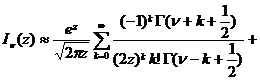
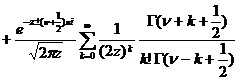
![]() fixed,
fixed,![]()
In the formula, the “ ” sign is selected as follows: at that time , take the positive sign, when,![]()
![]()
![]()
Take a negative sign .
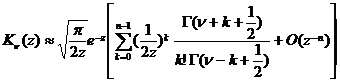
![]()
![]()
![]()
![]()
![]()
![]()
![]()