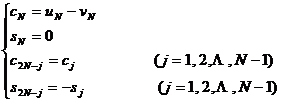§5   Fast Fourier Transform

 

1.         Finite discrete Fourier transform

 

[ Various Forms of Finite Discrete Fourier Transform ]

 

real (or complex) sequence f ( kh )	Finite discrete Fourier transform and its inversion formula	hd
( N is a positive integer)
( N is a positive integer)
( k , N is an integer)

 

    [ Convolution and its properties ]   Let the real (or complex) sequence g ( kh ) be a sequence with period Nh , which is called

                    

is the convolution of the sequences f and g . Let

                      

                                

then                    

                      

 

Second, the     fast Fourier transform algorithm

 

    The Fast Fourier Transform ( FFT ) algorithm is a fast method for computing finite discrete Fourier transforms .

    [ FFT algorithm of complex sequence ] To calculate the finite discrete Fourier transform of the complex sequence { z _k } , is to calculate the form 

                    ,   

The finite term sum of . For the inversion formula, the calculation method is similar .

    Let N = 2 ^m , ,   then

                           

set again                 

                     

are the binary representations of k and j , respectively , and take the value 0 or 1. Then

             

because =   

                       =

                       =

so

   

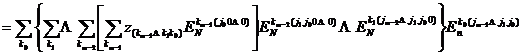
This leads to the recursive formula:

                  

                

                

                

                  

                

                

Finally there is

                

[ FFT Algorithm for Real Sequences ] Finite Discrete Fourier Cosine Transforms and Sine Transforms to be Calculated for Real Sequences with 2 N ( N = 2 ^m ) Elements  

                      

                      

The FFT algorithm can be used first for complex sequences

                  z _k =x _k +iy _k         

calculate

                      

And c _j , s _j use the following formula to find

  

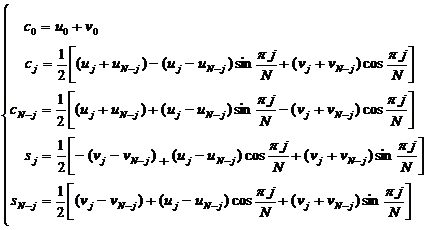
As for c _j , the value of s _j is when